Музыкальные интервалы | Сведение аудио

Музыкальные интервалы начал исследовать еще Пифагор. Понять сущность интервалов лучше всего в звуковых примерах и графиках амплитудно-частотной характеристики.

Музыкальные интервалы бывают:

мелодическими, когда два звука звучат в разное время;
гармоническими, когда они звучат одновременно.

Если один звук был взят раньше, а потом к нему добавился другой, то (в зависимости от контекста) их можно рассматривать и как мелодический, и как два гармонических интервала.

Для измерения качественной величины музыкальных интервалов (их абсолютного значения вне музыкального лада) обычно используют:

Октавы – соотношения частот звуков 2/1
Тоны – соотношения частот ⁶²= 1,1224620483093729814335330496792…
Полутоны – соотношения частот ¹²²= 1,0594630943592952645618252949463…
Центы – 1/100 полутона = 1,0005777895065548592967925757932…

В примере октава, тон, полутон и цент в гармоническом соединении:

Количественная величина интервала описывает количество ступеней лада составляющих интервал. С некоторым упрощением, под ладом пока будем понимать совокупность звуков, на которых строится мелодия. В большинстве случаев в основе музыки лежит так называемая диатоника – лад из семи ступеней, а расстояние между ступенями, как правило, равно полутону или тону.

интервал	прима	секунда	терция	кварта	квинта	секста	септима	октава
количество ступеней	1	2	3	4	5	6	7	8

У тех, кто впервые сталкивается с ладом и интервалами, возникает недоумение, почему считая ступени, мы считаем их количество, а не расстояние между ними. То есть, примой называется два совпадающих звука, находящихся на одной ступени, а не два звука расположенных на расстоянии в одну ступень лада. Но, такова специфика интервалов. Их названия как раз и происходят от перефразированных латинских числительных, указывающих число ступеней, а обозначаются они соответствующей цифрой.

Разные по названию интервалы могут иметь одинаковую качественную величину. Такие интервалы называют энгармонически равными. Чтобы указать качественную величину интервала их называют чистыми, большими, малыми, уменьшёнными и увеличенными.

Энгармоническое равенство интервалов:

Величина в полутонах:	уменьшённые	малые	чистые	большие	увеличенные
0	ум2уменьшённая секунда		ч1чистая прима
1		м2малая секунда			ув1увеличенная прима
2	ум3уменьшённая терция			б2большая секунда
3		м3малая терция			ув2увеличенная секунда
4	ум4уменьшённая кварта			б3большая терция
5			ч4чистая кварта		ув3увеличенная терция
6(тритон)	ум5уменьшённая квинта				ув4увеличенная кварта
7	ум6уменьшённая секста		ч5чистая квинта
8		м6малая секста			ув5увеличенная квинта
9	ум7уменьшённая септима			б6большая секста
10		м7малая септима			ув6увеличенная секста
11	ум8уменьшённая октава			б7большая септима
12			ч8чистая октава		ув7 увеличенная септима

Причина того, что интервалы одной качественной величины имеют два названия, лежит в том, что вне лада они просто являются диссонансами и консонансами. Внутри музыки, они приобретают ладовую напряженность (становятся устойчивыми и неустойчивыми). Уменьшённые интервалы вызывают у слушателя потребность в том, чтобы их звуки переместились («разрешились») в еще более близко расположенные друг к другу («устойчивые» I, III и V ступени лада). Увеличенные – в более широко расположенные. Обратный случай вызывает у слушателя психологическое ощущение отказа от цели. То есть интервалы стали уменьшенными (увеличенными) как бы на полпути к ощущению устойчивости (разрешению).

Чистые, большие и малые интервалы, так же в ладу могут оказаться на неустойчивых ступенях, но направления движения составляющих их звуков не вызывают подобных ощущений.

Интервалы, которые бывают малыми и большими никогда не называют чистыми. Чистые – не могут быть малыми или большими. Здесь сказывается старинная традиция, возникшая во времена, когда к консонансам относили только приму, октаву, квинту и кварту. До сих пор сохранилась традиция делить консонансы на:

весьма совершенные: ч1, ч8
совершенные: ч4, ч5
несовершенные: м3, б3

Более того, кварта и квинта так же сильно различаются по отношению к ним теории и гармонии. Параллельное движение совершенными консонансами и чистыми квинтами подчеркнуто создает пустое звучание (потому в классической гармонии запрещено), чего не наблюдается у кварт. Кроме того существует традиция считать кварту, построенную на главной ступени трезвучия – диссонансом.

Интервалы шире двух октав именуют, как и простые, добавляя количество октав (например «чистая кварта через три октавы»). Интервалы до двух октав имеют собственные имена. Интервалы шире октавы называют составными:

нона = секунда через октаву

децима = терция через октаву

ундецима = кварта через октаву

ундецима = квинта через октаву

терцдецима = секста через октаву

квартдецима = септима через октаву

квинтдецима = 2 октавы

Обращением интервалов называется такое перемещение их звуков, при котором нижний – становится верхним. То есть терция перемещается в сексту, нона в септиму и квартдециму. Чистые интервалы при этом остаются чистыми, малые обращаются в большие, а большие в малые.

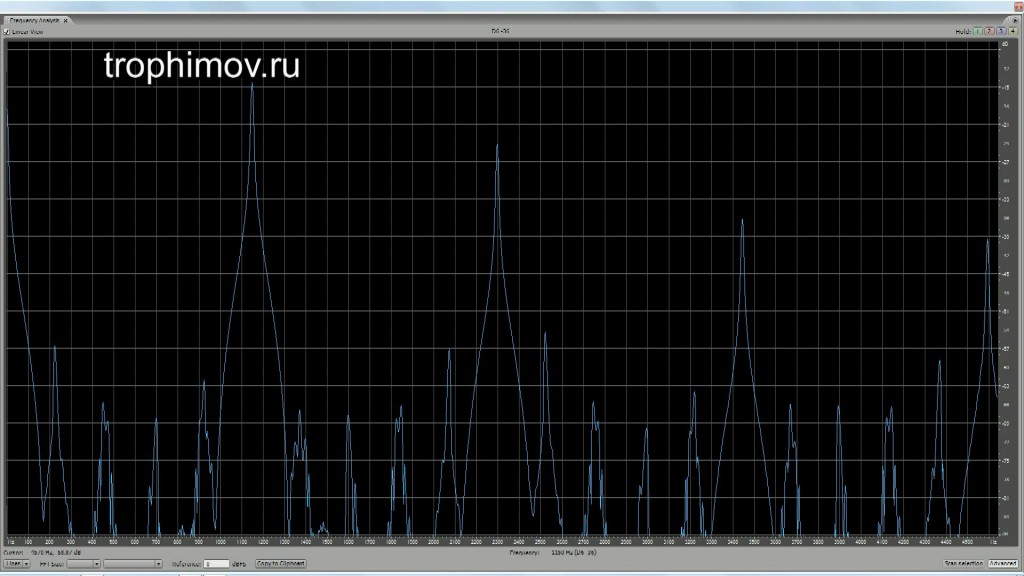
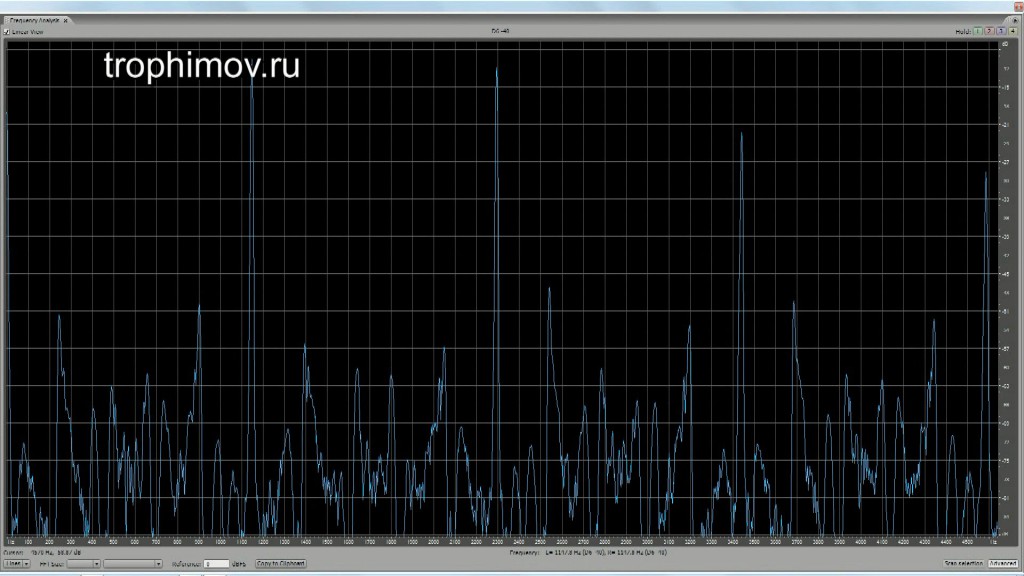
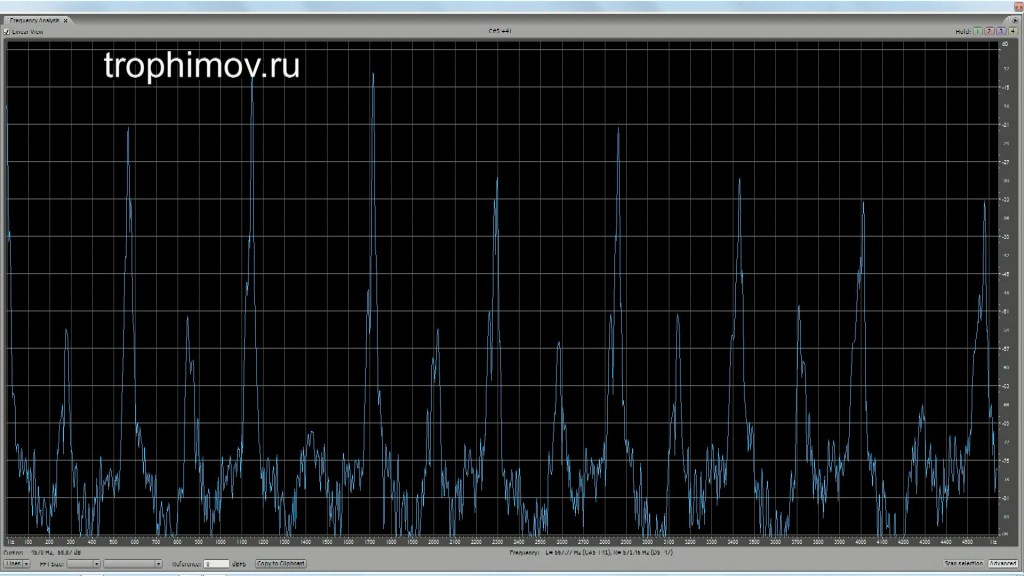
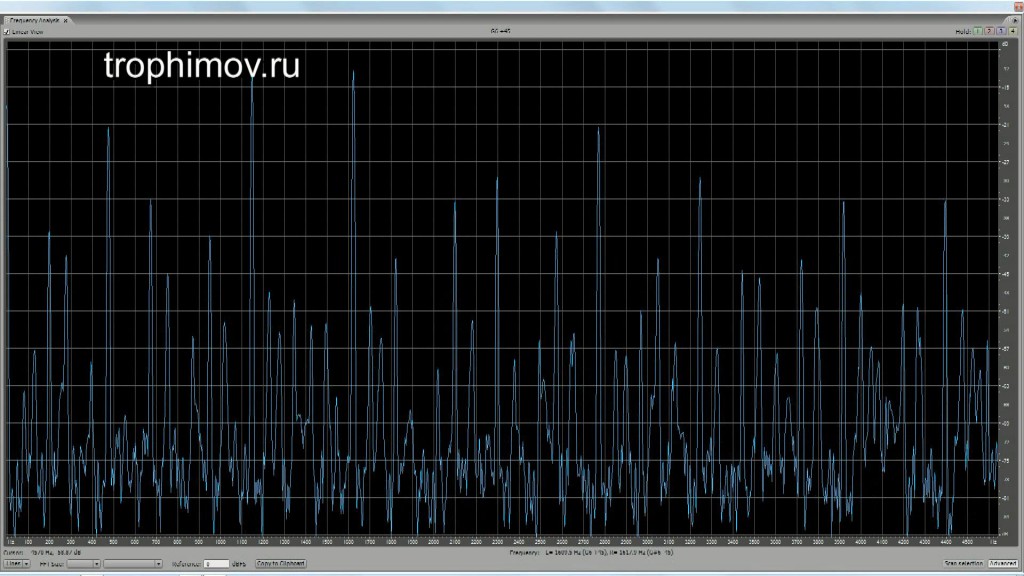
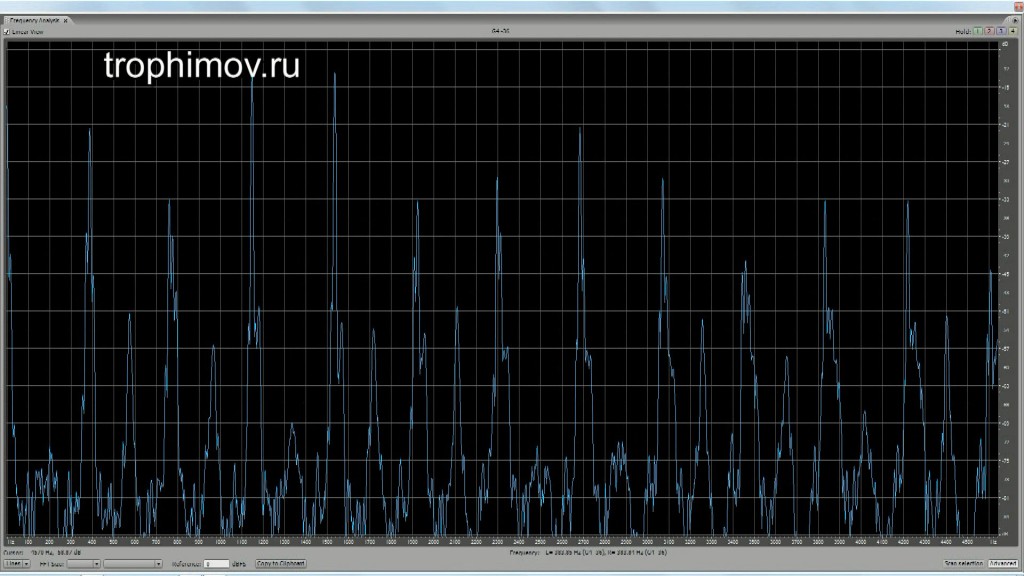
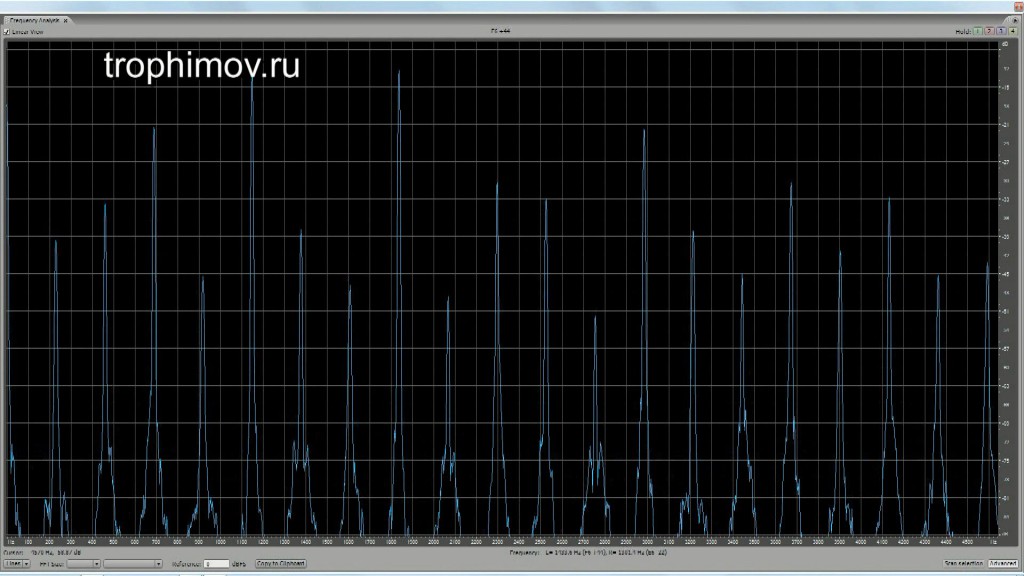
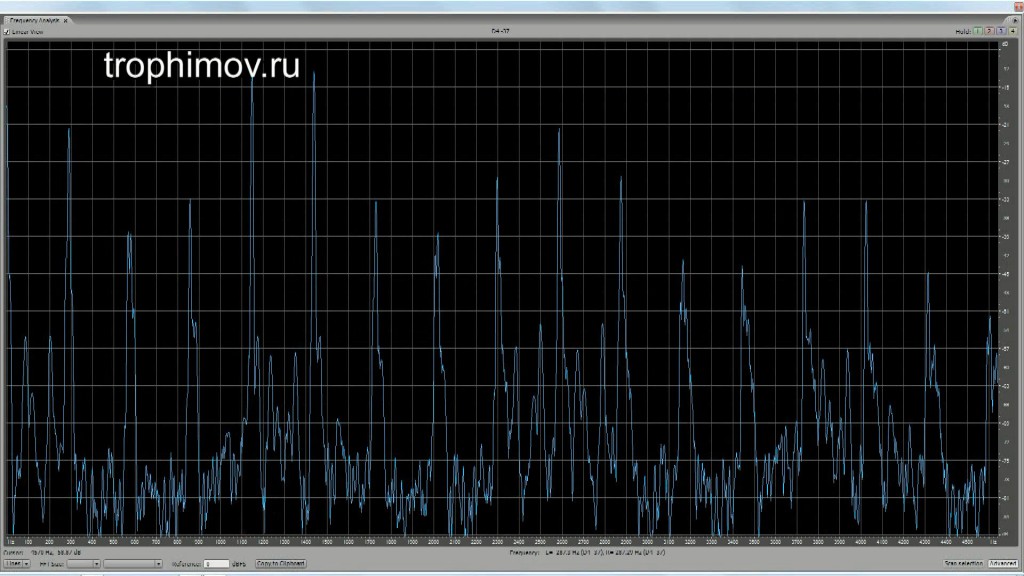
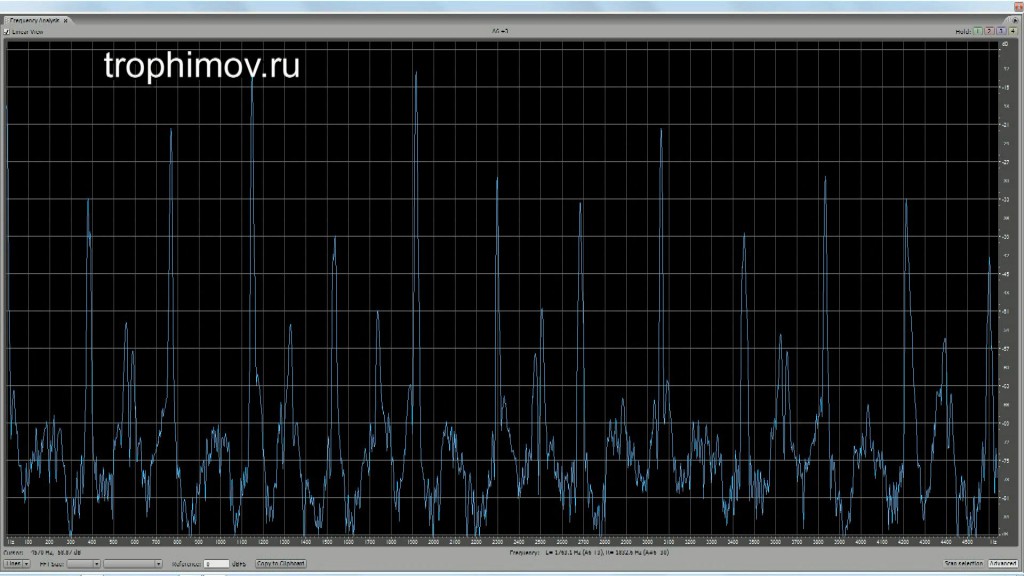
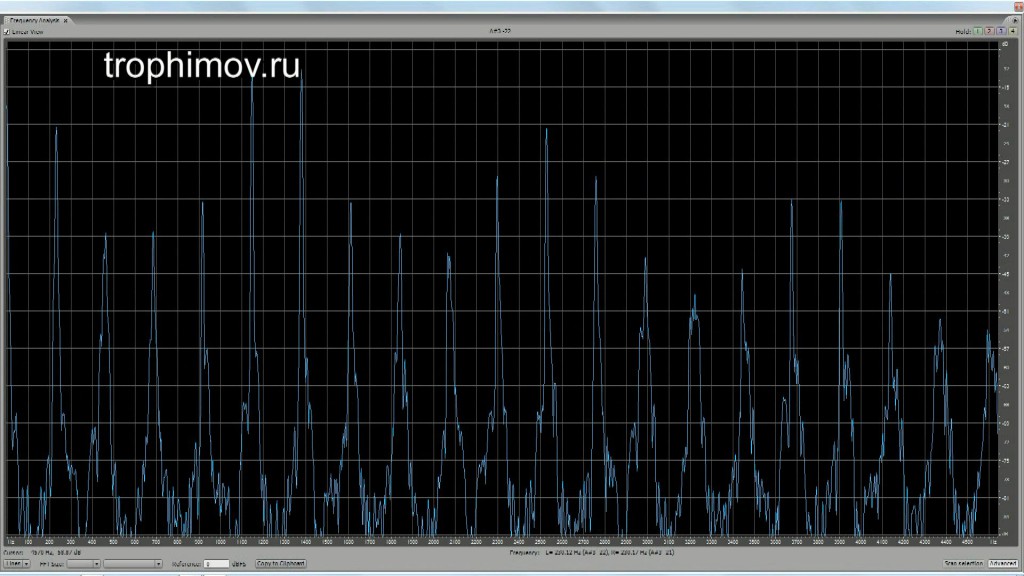
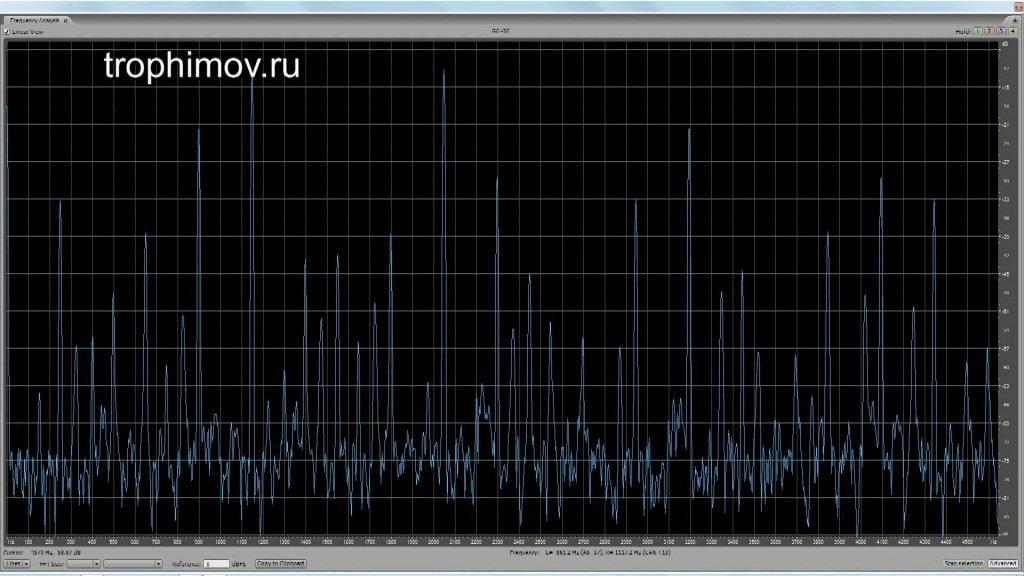
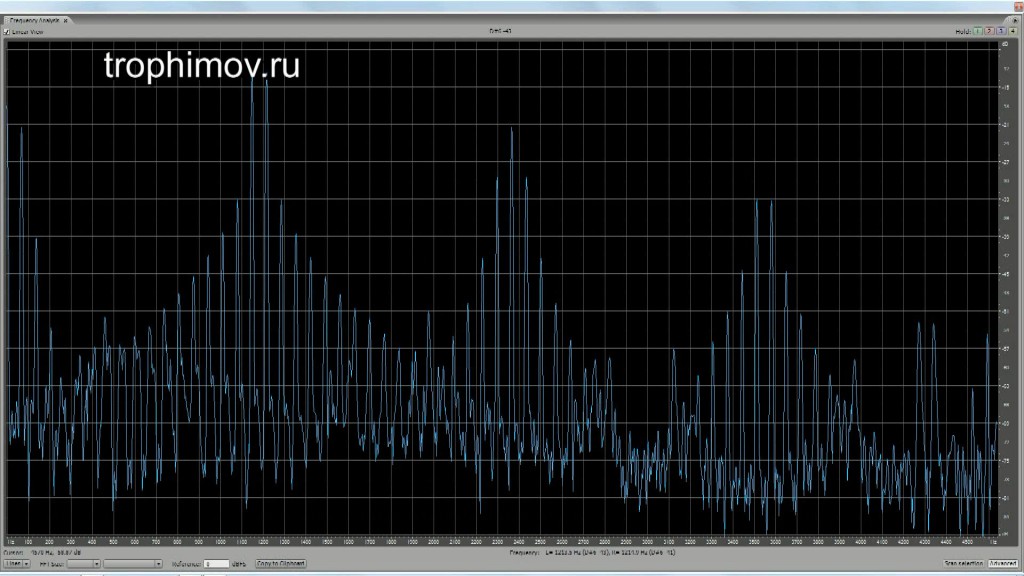
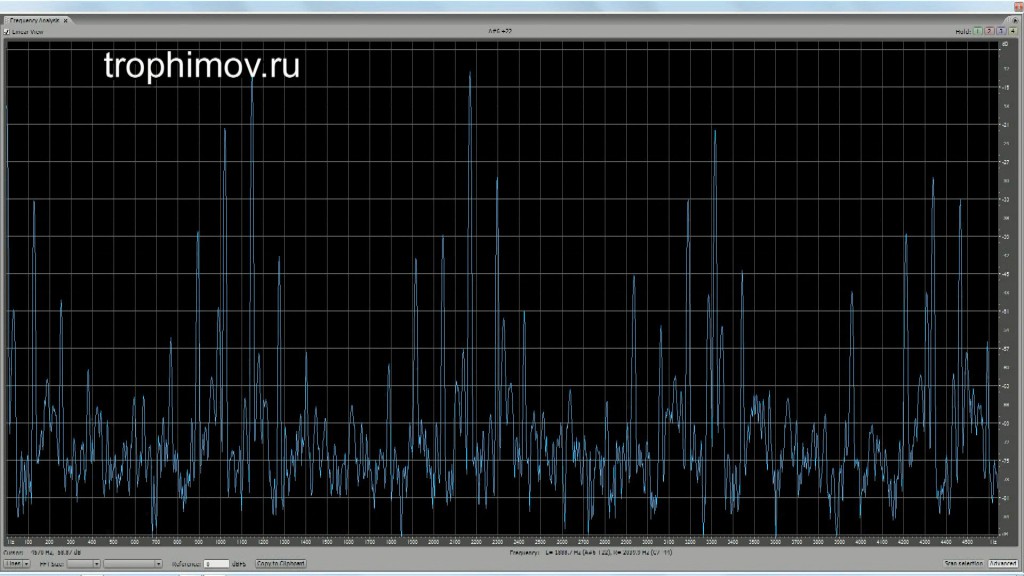
Графики АЧХ консонирующих интервалов с учетом искажений при восприятии:

Чистая прима (четко видны только пики, совпадающие с обертонами):